I need a way to determine what an instance’s italic angle will be when exported to a font binary. If it has the Italic Angle custom parameter, that’s easy. But otherwise Glyphs seems to interpolate the italic angle based on the angles of the masters that instance is based on. For a single-axis design space this would be pretty straightforward to calculate myself, but if more than 2 masters are influencing the instance’s italic angle it gets complicated. Is that Euclidean math? ![]() I just want to respect how Glyphs calculates/derives the italic angle during export. Would it be possible to add a read-only italicAngle property to GSInstance? Or can you share a reliable way for my script to calculate it?
I just want to respect how Glyphs calculates/derives the italic angle during export. Would it be possible to add a read-only italicAngle property to GSInstance? Or can you share a reliable way for my script to calculate it?
Thanks!
When exporting to binary, it looks like Glyphs calculates post::italicAngle by applying interpolation to the value in Masters > Metrics > Italic Angle. It does not output the true angle, which is usually slightly different from the interpolated angle. So the easiest solution I can think of is using GSInstance.interpolatedFontProxy, something like this:
inst = Glyphs.font.instances[idx]
proxy = inst.interpolatedFontProxy
print(proxy.masters[0].italicAngle)
That’s a great idea, @justinpenner! I hadn’t thought of that. @GeorgSeifert or @mekkablue, is that my best option?
Can you show an example? (e.g. a .glyphs file where that happens).
Sure, here’s a quick test font with one /H glyph:
slantAngleTest.zip (219.2 KB)
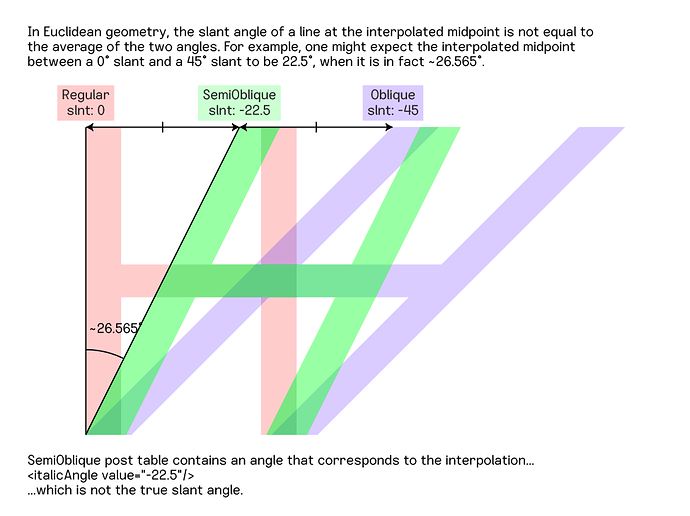
And here is a drawing that explains the problem I’m referring to. I don’t know the name of this phenomenon but I’ve seen it discussed here once or twice before.
It sounds like that would affect variable fonts with a slant axis too—right? I suppose you could compensate for it in a VF by adjusting the Axis Mapping custom parameter (for the avar table).
That’s correct, it would affect variable fonts, too, and you could theoretically write a script that automatically generates avar entries to compensate for this effect, not perfectly but to a certain level of precision. But most fonts aren’t slanted more than around 16 degrees, and within that range the difference that this effect causes is very small.
Here’s another thread where a very similar problem is discussed. Due to essentially the same effect, if you slant a rectangle by 6 degrees, twice, the slant angle will not be 12°. Rather, it will be slightly less: ~11.87°. It’s easier to visualize this problem if you imagine applying a slant transformation of 45° to a rectangle, twice in a row. Of course it won’t result in a 90° slant, since a 90° slant isn’t possible.